At the MICRO 2023 conference, we demonstrated the invention of a new type of process-in-memory device “Random Increment Memory (RIM)” and applied it to the stochastic computing (unary computing) architecture.
In academia, PIM is currently a hot research field, and researchers often place great hopes on breaking through the von Neumann bottleneck with subversive architecture. However, the concept of PIM has gradually converged to specifically refer to the use of new materials and devices such as memristors and ReRAM for matrix multiplication. In 2023, from the perspective of outsiders like us who have not studied in PIM before, PIM has developed into a strange direction: yet developed PIM devices can process neural networks and simulate brains, but still unable to do the most basic operations such as counting and addition. In the research of Cambricon-Q, we left a regret: we designed NDPO to complete the weight update on the near-memory side, but it was unable to achieve true in-memory accumulation, so the reviewer criticized “it can only be called near-memory computing, not in-memory computing.” From this, we began to think about how to complete in-place accumulation in the memory.
We quickly realized that addition could not be done in-place with binary representation. This is because although addition is simple, there is carry propagation: even adding 1 to the value in memory may cause all bits to flip. Therefore, a counter requires a full-width adder to complete the self-increment operation (1-ary successor function), thus all data bits in the memory must be activated for potential usage.
Fortunately, the self-increment operation results in only two bit flips on average. We need to find a numeral representation that limits the number of bits flipping in the worst case. Therefore we introduced Skew binary number system to replace binary numbers. The skew binary was originally proposed for building new data structures, such as the Brodal heap, to limit the worst-case time complexity when a heap merges. It is very similar to the case here, that is, limiting carry propagation.
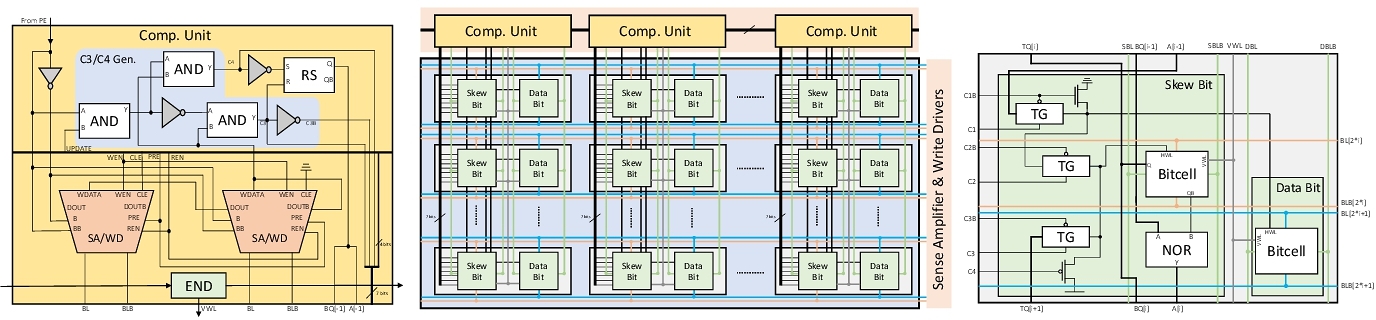
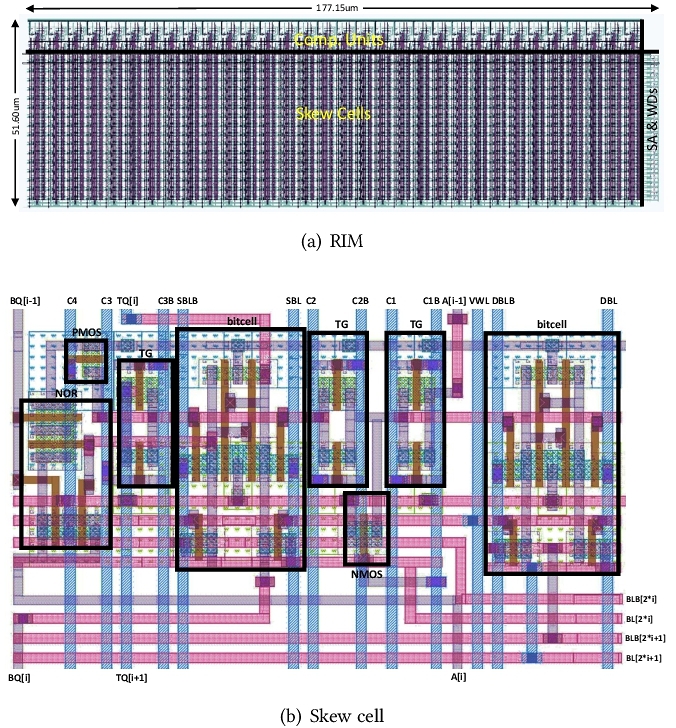
We base on SRAM in conventional CMOS technology to design RIM. We store digits (in skew binary) in column direction, and use an additional column of SRAM cells to store the skew bit of each digit (that is, where the digit “2” is in the skew number). The self-increment operations are performed as follows:
- If any digit in the current skew number is “2”, set “2” to “0” and increase the next digit by 1;
- Otherwise, increase the least significant digit by 1.
Although the row-index of “2” in each skew number are different (the skew counting rules promise that at most one digit can be “2”), the cells to be operated on will be randomly distributed in the memory array. It cannot be activated according to the row selection of SRAM. But we can use the latched skew bit to activate the corresponding cells to operate, so that cells located in different rows can be activated in the same cycle!
Finally, we achieved a 24T RIM cell. Not using new materials, but built entirely from CMOS. RIM can process random self-increment on stored data: in the same cycle, each data can self-increment or remain unchanged on demand.
We apply RIM in stochastic computation (unary computation). A major dilemma in stochastic computing is the cost of conversion between unary numbers and binary numbers. Converting binary numbers to unary numbers requires a random number generator, and converting back requires a counter. Because unary numbers are long (up to thousands of bits), after computing in unary, the intermediate results must be converted back to binary for buffering. As a result, counting operations can account for 78% energy consumption. We use RIM to replace the counters in uSystolic and propose the Cambricon-U architecture, which significantly reduced the energy consumption of counting operations. This work solves a key problem of stochastic deep learning processors, boosting the application of these technologies.