随着大语言模型的兴起,受算力和存储预算所限,4比特量化模型正成为大语言模型部署的首选。然而,我们观察到,传统计算架构在处理低精度矩阵乘法时存在严重的计算冗余问题。 我们提出Cambricon-C架构,通过创新的 原初化矩阵乘法(Primitivized MM) 算法,有望彻底改变4比特矩阵计算的实现方式。
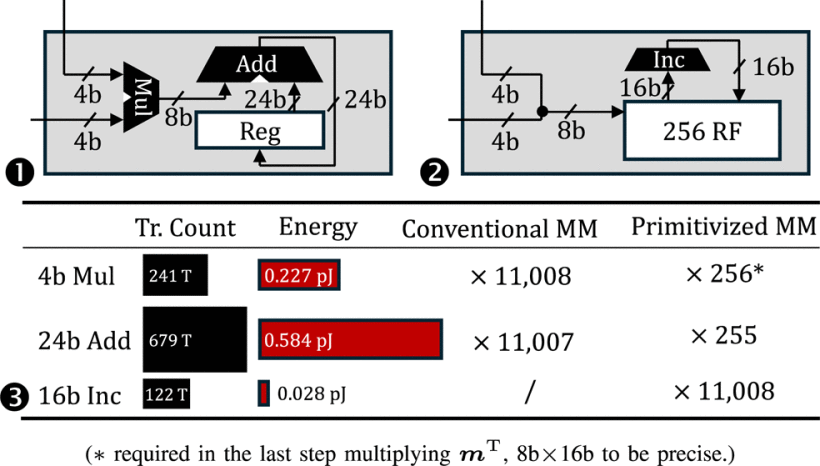
对4比特矩阵乘法的运算过程进行深入分析,就会发现惊人的冗余:在Llama2-7B的4比特量化版本中,完成单个输出神经元激活值需要计算11,008次4比特乘法并累加到一起。而4比特数据最多仅有16种可能值,根据鸽笼原理,超过97%的乘法必然是重复发生的。传统基于MAC单元设计的矩阵运算器会重复计算这些相同乘积,意味着巨大的能耗浪费。
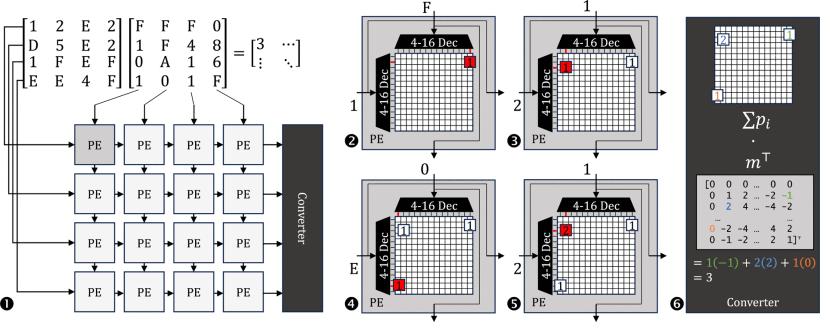
PMM算法则提出:根据乘累加运算的逆分配律,先统计各项乘法出现的次数,最后统一加权求和,大幅削弱计算强度。
- 预计算消除重复乘法:预先计算所有可能的4比特乘积组合(共256种),表示为查找表。实际计算时只需查表而非重复计算。
- 加法强度降低:将累加操作转化为对256个计数器的增量操作,用一元后继运算(即计数)替代传统加法树,显著削减了加法的强度。
基于PMM算法,我们设计了Cambricon-C架构:
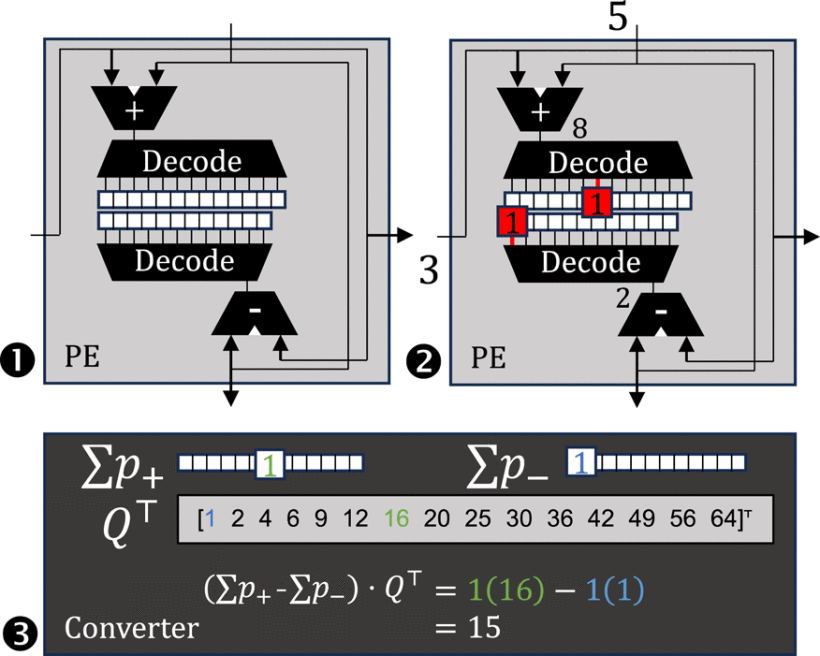
- 四分平方法(QSM):我们重新探索了源自19世纪的四分平方乘法,在此将计数器数量从256个减少到29个(称为“R29方案”),面积效率提升8.6倍。
- 行波计数器:采用自定时D触发器链实现计数器,相比SRAM方案动态功耗降低51%。
实验结果显示:
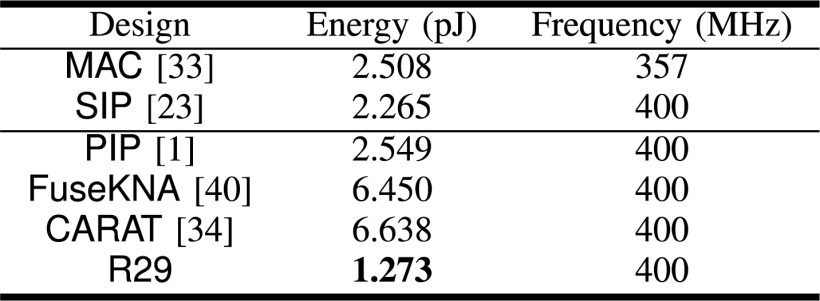
- 单个PE能效达传统MAC单元的1.97倍
- 32×32阵列完整加速器在LLaMA2推理中实现1.25倍端到端能效提升
- 性能优势随矩阵规模增大而提升
Cambricon-C开创了”原初化运算”的新范式,通过将复杂运算分解为最基础的计数操作,我们重新探寻了低精度计算的效率极限: 未来加速器的运算效率不再取决于精巧的MAC单元设计,而需要将整个矩阵运算通盘考虑、整体优化。 在不远的将来我们还将公开发表更多关于“原初化运算”的工作,持续推动深度学习处理器底层微架构的革新,希望获得各位同行关注。