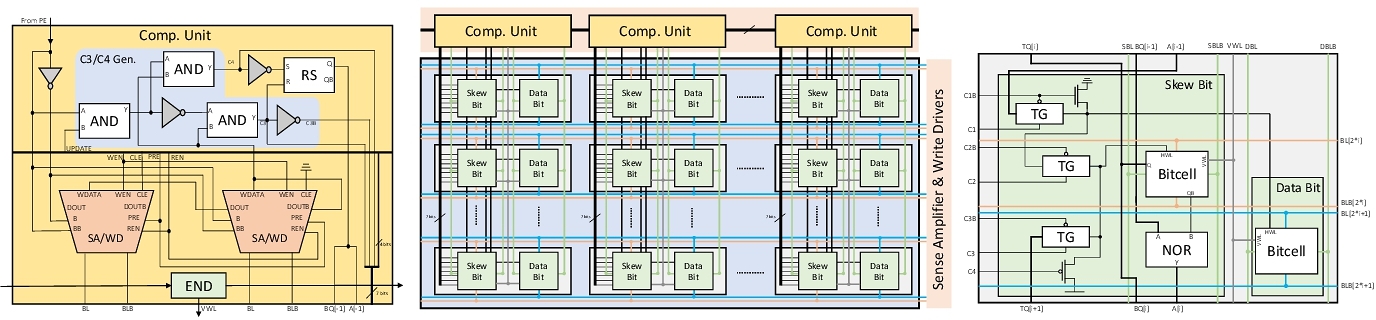
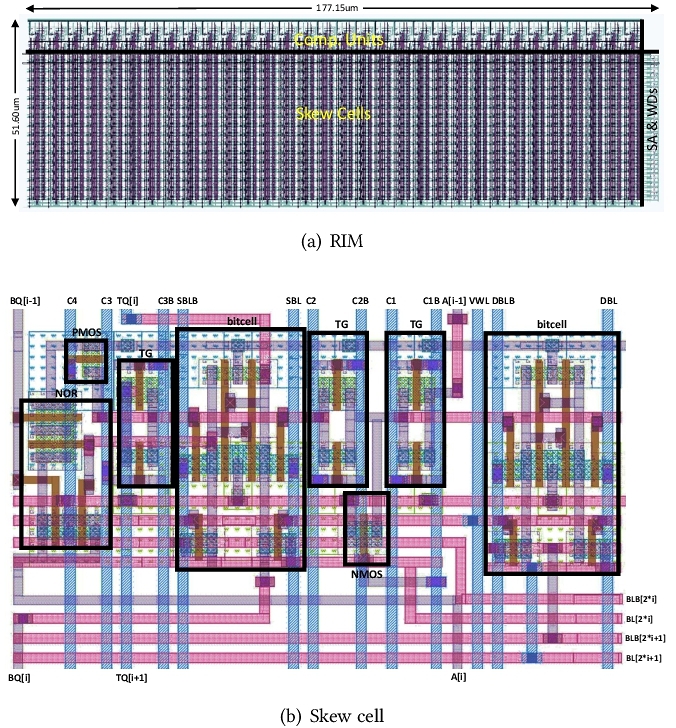
在MICRO 2023大会上,我们展示发明了一种新型存内计算器件“随机自增存储器(RIM)”,并将其应用于随机计算(一进制计算)架构中。
在学术界,存内计算是当前火热的研究领域,常被研究者寄予突破冯·诺依曼瓶颈、实现计算机体系结构大变革的美好期望。 但目前,存内计算这一概念的涵义却逐渐收敛于特指采用忆阻器、阻变存储器(ReRAM)等新材料、新器件完成矩阵计算这种特定计算功能。 在2023年,在我们这些原来并不研究存内计算的外行研究者看来,存内计算发展到了一个很奇怪的境地:已经发展出的存内计算设备能够很好地处理神经网络、功能类比大脑,却仍然无法做诸如计数、加法这样最基础的运算。 在Cambricon-Q的研究中,我们留下了一个遗憾:我们设计了NDPO在近存端完成权重更新,却无法做到真正的存内累加,因此被评阅人批评“只能称为近存计算,而非存内计算”。 由此,我们开始了对于如何在存储器内完成原位累加的思考。
我们很快意识到,如果采用二进制记数,加法是很难在存储器内原位完成的。 这是因为加法虽然简单,但存在进位传播:即使是对存内数值加1,也有可能导致所有比特全部发生翻转。 因此,在集成电路中制作计数器,需要一个完整的加法器来完成数值自增操作(后继运算),存储器内完整的数据必须全部被激活备用。
好在自增操作在平均情况下只会导致两个比特的翻转。我们需要找到一种记数法,控制最差情况下可能发生翻转的比特数量。因此我们引入了偏斜二进制记数法来代替二进制。偏斜记数法最初提出时是用于数据结构设计,例如用于Brodal堆,控制堆发生归并时的最差情况时间复杂度,而这与控制加法的进位传播十分类似。
我们使用CMOS上的SRAM技术作为基础来设计RIM。我们将存储的数值(以偏斜记数法记录)按列向存储,并为每一列额外提供一列SRAM单元格用来存储每一数位的偏斜状态(即偏斜数中的数位“2”)。偏斜数的自增操作规则如下:
- 如果当前数中有数位为“2”,将“2”置“0”,将其下一位增1;
- 否则,将最低位增1.
虽然每一个数中的“2”所处的行可能不同(偏斜记数规则中要求一个偏斜数中最多只能有一位为“2”),导致要操作的单元格随机分布在存储器阵列里,不能按以往SRAM的行选方式来激活;但我们可以使用上一位的偏斜状态来激活本位和下一位的对应单元,实现在同一操作周期中激活出位于不同行的单元格!
最终,我们实现了24T的RIM单元格——没有使用新材料,而是完全由CMOS技术构建。RIM能够实现对所存数据的随机自增:在同一操作周期里,RIM所存储的一些数据可以按需自增,而其他数据可以保持不变。
我们将RIM应用于随机计算(一进制计算)中。 随机计算的一大痛点在于一进制数与二进制数之间的转化开销——二进制数转一进制数需要随机数发生器,一进制数转二进制数需要计数器。因为一进制数数位太长(可达上千比特),使用一进制数完成计算后,中间结果如需暂存,必须转换回二进制,使计数操作所消耗的能量甚至能达到整个计算架构的78%。 我们使用RIM替换了uSystolic中的计数器,构建了Cambricon-U架构,显著降低了计数操作的能耗。 这项工作解决了基于随机计算的深度学习处理器的一项关键痛点,使相关技术有望更快应用。