(ZH-EN Translation by DeepSeek-V3-0324)
With the rise of large language models, 4-bit quantized models have become the preferred choice for deployment due to computational and storage budget constraints. However, we observe that traditional computing architectures suffer from significant computational redundancy when handling low-precision matrix multiplication.
We propose the Cambricon-C architecture, which aims to revolutionize the implementation of 4-bit matrix computation through an innovative Primitivized Matrix Multiplication (PMM) algorithm.
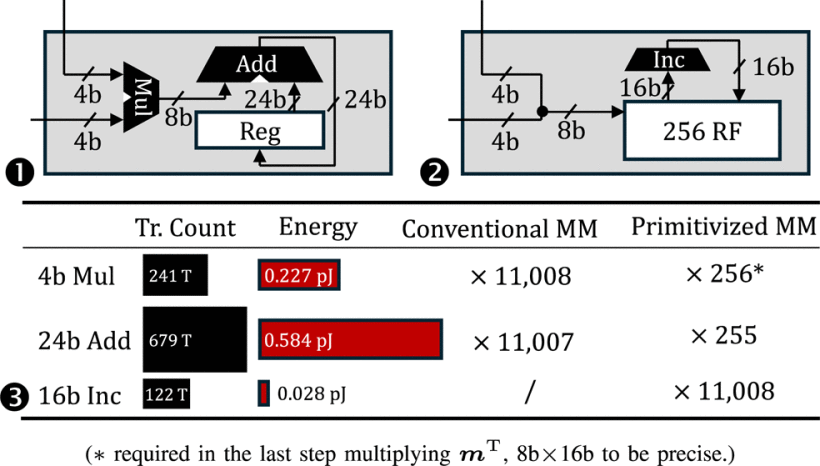
An in-depth analysis of 4-bit matrix multiplication reveals astonishing redundancy: in the 4-bit quantized version of Llama2-7B, computing the activation value of a single output neuron requires 11,008 4-bit multiplications followed by accumulation. Since 4-bit data has at most 16 possible values, the pigeonhole principle dictates that over 97% of these multiplications must be repeated. Traditional matrix processors based on MAC units redundantly compute these identical products, resulting in enormous energy waste.
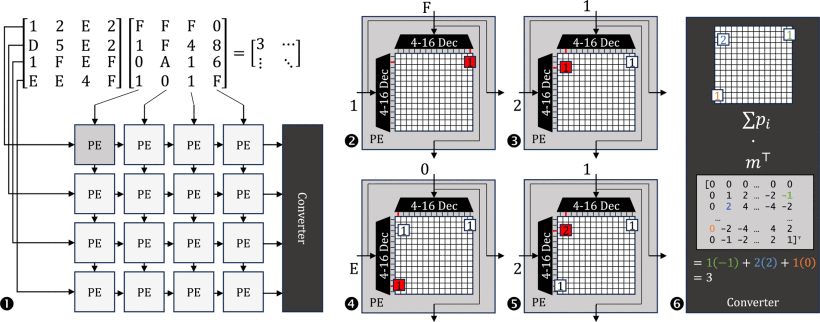
The PMM algorithm proposes: By leveraging the inverse distributive property of multiply-accumulate operations, we first count the occurrences of each multiplication and then perform a unified weighted summation, significantly reducing computational intensity.
- Precomputation to Eliminate Redundant Multiplications: Precompute all possible 4-bit product combinations (256 in total) as a lookup table. During actual computation, only table lookup is required instead of repeated calculations.
- Reduced Addition Intensity: Transform accumulation operations into incremental updates of 256 counters, replacing traditional adder trees with unary successor operations (i.e., counting), drastically cutting addition overhead.
Based on the PMM algorithm, we designed the Cambricon-C architecture:
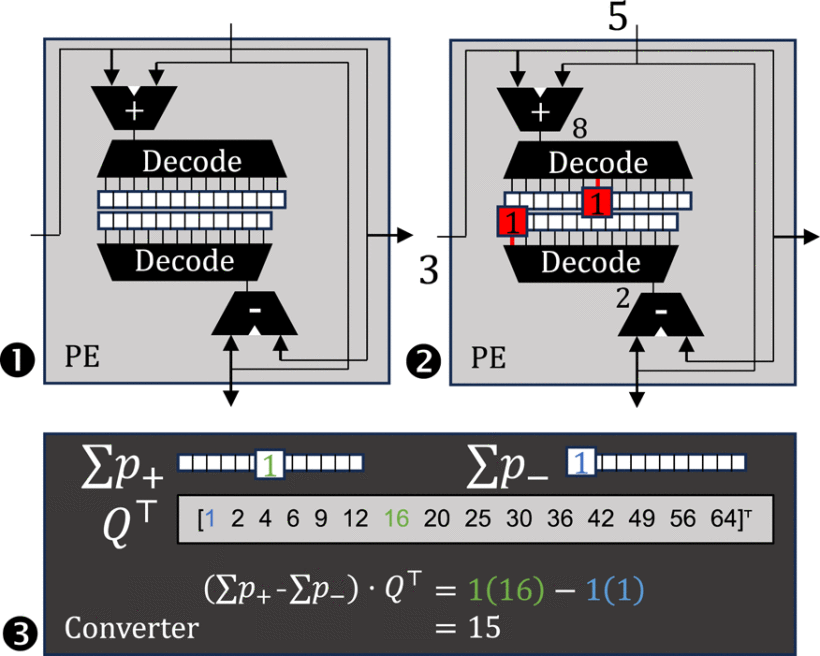
- Quarter-Square Multiplication (QSM): We revisited the 19th-century quarter-square multiplication technique, reducing the number of counters from 256 to 29 (referred to as the “R29 scheme”), achieving an 8.6× improvement in area efficiency.
- Ripple Counters: Implemented counters using self-timed D flip-flop chains, reducing dynamic power by 51% compared to SRAM-based solutions.
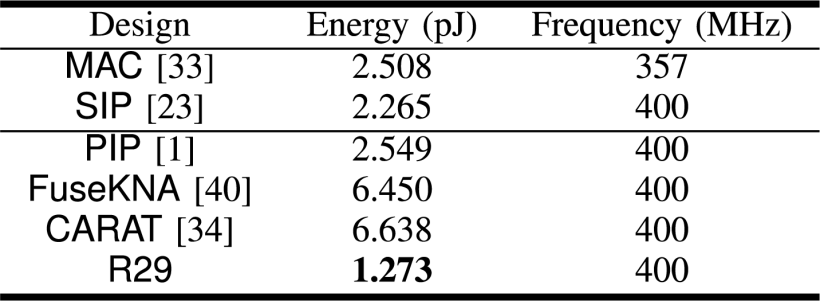
Experimental results show:
- A single PE achieves 1.97× higher energy efficiency than traditional MAC units.
- A full 32×32 array accelerator delivers a 1.25× end-to-end energy efficiency improvement for LLaMA2 inference.
- Performance advantages scale with matrix size.
Cambricon-C pioneers a new paradigm of “primitivized computation”. By decomposing complex operations into fundamental counting operations, we redefine the efficiency limits of low-precision computing:
The future efficiency of accelerators will no longer depend on intricate MAC unit designs but rather on holistic optimization of entire matrix operations.
In the near future, we will publish more work on “primitivized computation”, continuing to drive innovation in the microarchitecture of deep learning processors. We welcome attention and collaboration from peers.